TransLight

Image-Guided Customized Lighting Control with Generative Decoupling

Abstract

现存的大多数光照编辑方法不能够提供定制的光影效果和保留内容整体性。这使得这些方法对于如何将推理图像的光照迁移到用户指定的图像这一复杂任务的表现很不好。为了解决这个问题，本文提出了 TransLight，一个能够实现高保真以及高自由度光影迁移的新颖方法。从推理图像中提取光影风格是本文最具挑战性的一步。难点在于光影中的复杂的几何结构特征是与真实世界图像的内容信息高度耦合的。为了实现这一目标，本文首先提出了生成式解耦技术，即使用两个经过微调的扩散模型来精确分离图像内容和光影，从而生成一个全新整理的、百万级的图像-内容-光三元组数据集。然后，本文采用 IC-Light 作为生成模型，并用三元组训练模型，并注入参考光照图像作为额外的调节信号。由此产生的 TransLight 模型能够实现各种光影的定制化和自然迁移。值得注意的是，通过彻底分离光影与参考图像，本文提出的生成式解耦策略赋予了 TransLight 高度灵活的照明控制能力。实验结果证明，TransLight 是首个能够成功在不同图像之间迁移光效的方法，它比现有技术能够提供更个性化的照明控制，并为照明协调和编辑领域的研究指明了新的方向。

Introduction

Method

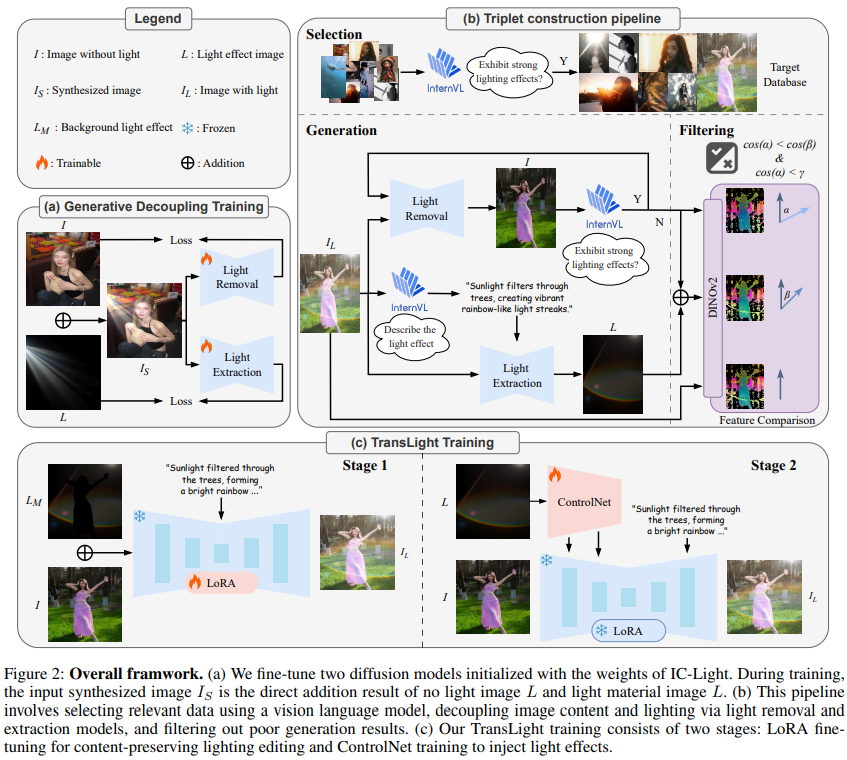
如图 2 所示，该图系统地说明了本文的框架是如何进行光影迁移的。该框架包含三个主要组件：用于生成解耦的训练模型，图像-内容-光三元组的构建流程，以及 TransLight 的训练。

Generative Decoupling

图 2 (a) 展示了该部分的训练策略。首先使用 InternVL2.5 从大量数据库中选择 1M 张不包含光影的图片。然后，收集 100K 张 Light Material 图像，其中 90K 张生成自 FLux.1-schnell, 10K 收集自公开数据集。在这之后，微调IC-Light。 对于无光影图像 $I$ 和 Light Material 图像 $L$ 的合成，并不需要太多的复杂操作，可以由下面的公式表示：

\[\begin{equation} I_S = aI + bL, \end{equation}\]

其中 $a,b \sim U(0,1)$.

Image-content-light Triplet Construction Pipeline

如图 2 (b) 所示，数据构建流程包括 3 个步骤。

Selection. 本文从专有数据库（proprietary database）中挑选目标数据。首先，使用 InternVL2.5 来做大规模的数据选择。本文制定了严格的提示词来指导视觉语言模型判断每一张图像是否包含强烈的光影。

Generation. 使用去光照模型以及光照提取模型来将一张包含强烈阴影的图片分解为只包含内容的无光影图片和一张纯光影图片。在去光影过程中，使用 InternVL2.5 来评估生成的结果。如果结果不符合要求，会执行第二轮的去光影过程。在光影提取过程中，仍然使用 InternVL2.5 来生成光影图像的描述词。描述词结合源图像输入到光影提取模型中时，能够显著地提高模型分离光影的能力。

Filter. 本文执行基于相似度的筛选策略来丢弃生成质量不高的结果，以提高训练数据的质量。具体地，在将具有光影的输入图像 $I_L$ 分解为无光影图像 $I$ 和纯光影图像 $L$ 之后，我们使用公式 1 所表示的简单合成策略来得到 $I_S$, 在这里 $a$ 和 $b$ 都取值为1。然后使用 DINOv2 从 $I_S,I_L,I$ 中分别地提取特征以及计算这些特征的余弦相似度。具体的计算方法如下面的公式所示：

\[\begin{equation} cos(\alpha) =Sim_{cos}(\mathcal{D}(I_L),\mathcal{D}(I)), \end{equation}\] \[\begin{equation} cos(\beta) =Sim_{cos}(\mathcal{D}(I_L),\mathcal{D}(I_S)), \end{equation}\]

其中 $\mathcal{D}$ 表示 DINOv2 而 $Sim_{cos}$ 表示余弦相似度。由于目标是去除光影，因此需要求 $I$ 和 $I_L$ 的余弦相似度低于阈值 $\gamma$。同时，由于还希望能够清晰且明显地分离光影 $L$，因此需要求 $I_S$ 和 $I_L$ 之间的相似度要尽可能的高。这意味着这些特征的相似度需要满足下面的式子：

\(\begin{equation} (cos(\beta) > cos(\alpha)) \wedge (cos(\alpha) < \gamma), \end{equation}\) 其中阈值 $\gamma$ 设置为 0.98