Physically Controllable Relighting of Photographs

Physically Controllable Relighting of Photographs

Abstract

Physically Controllable Relighting

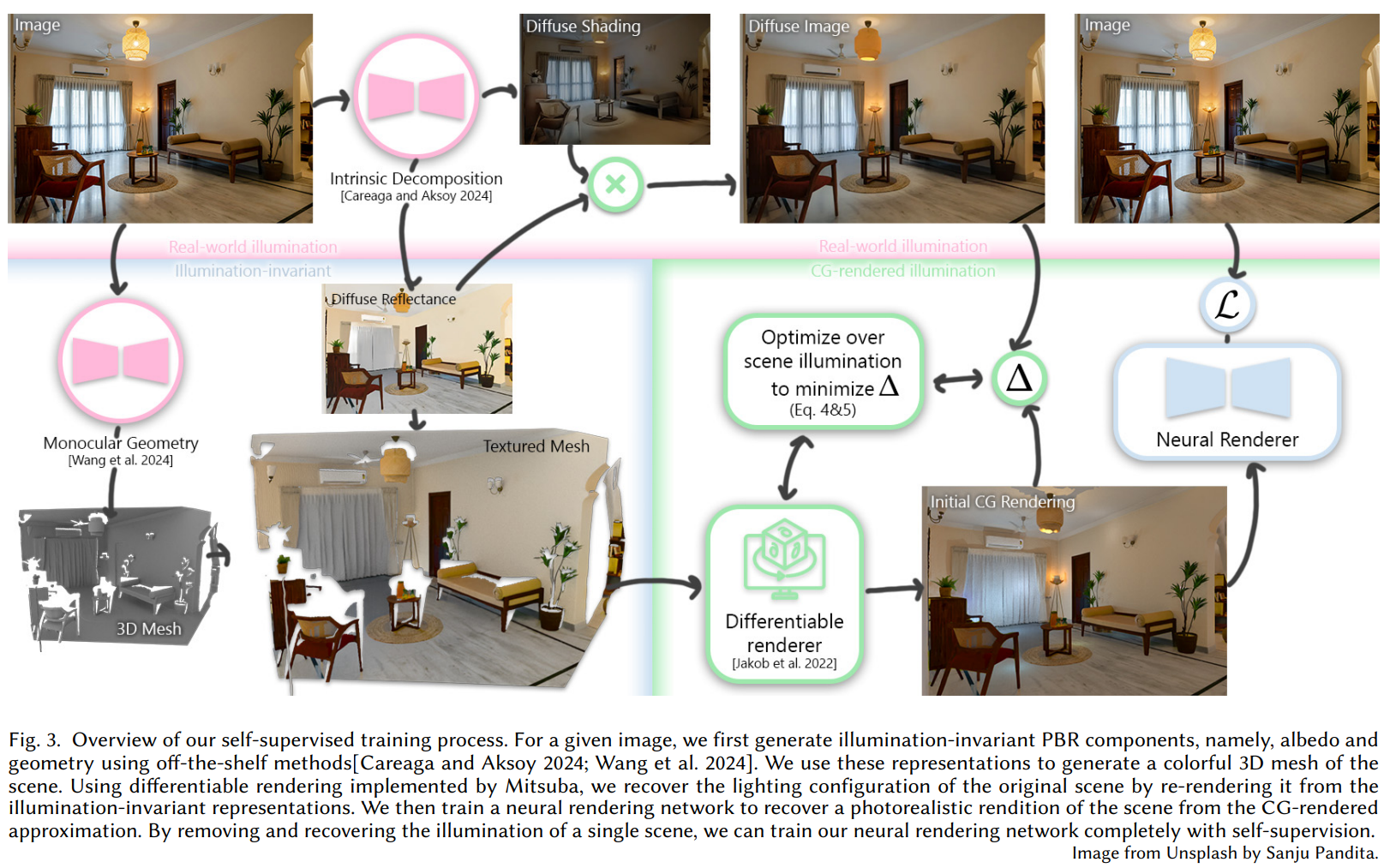
文本提出了一个能够将CG中对光源进行物理控制迁移到真实照片上的单图像重光照管线。为了让用户能够在 3D 渲染环境中控制光照，本文的首要任务是为输入的照片创建一个能够在 PBR 渲染引擎中使用的表示。这需要有对场景与光照无关的3D几何表示。

本文使用了单目几何估计方法 $\mathrm{MoGe}$ 来从单张图像中预测 3D 点云以及相机参数，本文还使用了本征图像分解方法 $\mathrm{CID}$ 来获得输入图像的 diffuse reflectance。$\mathrm{CID}$ 使用了 e intrinsic residual model， 能够将单张输入图像 $I$ 分解为 3 个本征层：

\[\begin{equation} I = A \times S + R, \end{equation}\]

其中 $\mathrm{A}$ 表示 diffuse reflectance 或者 albedo，$\mathrm{S}$ 表示 diffuse RGB shading， 以及 residual layer $\mathrm{R}$ 包括所有的 non-diffuses 组件，比如高光（specularities）。本文使用 $\mathrm{MoGe}$ 中的 3D 点云方法来生成 mesh，然后将 mesh 与 前面得到的 diffuse reflectance 组合以得到能够在渲染引擎中使用的 textured mesh。特别地，mesh（Geometry）以及 diffuse reflectance 都是与光照无关的，最后将这些光照无关的表示加载到 能够允许用户自定义添加光源的 3D 渲染引擎中。

本文将 neural render 的任务建模为来补偿前面从单目视角中得到的textured mesh的渲染结果以得到更加真实的结果。如图 2 所示，使用 PBR 工具以及通过 3D 渲染引擎（Blender 或者 Mitsuba）得到的初次渲染将作为下一阶段（neural render）的输入来得到最终的真实图像。

Self-supervised Neural Rendering

Neural Render 的主要任务是给定初次渲染的 PBR 结果，重新渲染得到更加符合真实世界外观的图像。neural renderer 需要在真实世界的GT数据上进行训练以渲染得到具备non-diffuses effects的真实结果。得到上节中提到的 textured mesh $M$ 以及输入照片 $I$ 后，在使用光线追踪的情况下，只缺少光源这一个条件。下面详细介绍对 3D 照明环境的优化，该环境将在训练期间充当用户自定义照明的替代。

Optimization via Differentiable Rendering

给定输入图像 $I$ 和光照不变的 $M$，目标是使用光线追踪pbr渲染 $I$ 的最佳近似值。为此，将 3D 光照环境估计公式化为一个优化问题。

Target variable. 由于 $M$ 只对 diffuse reflectance 进行了建模，且由于输入图像 $I$ 包含了 non-diffuse effects，这使得 $I$ 难以作为目标变量。这是因为 non-diffuse effects 比如高光通常会导致在图像中出现特别明亮的区域，这会影响优化过程。作为替代，在优化过程中使用漫反射图像 $D$ 作为目标变量。通过 $\mathrm{CID}$ 方法，可以使用公式 1 中定义的漫反射率 $𝐴$ 和漫反射阴影 $𝑆$ 来获取漫反射图像 $𝐷$ :

\[\begin{equation} D = A \times S , \end{equation}\]

Unknown variables. 不失一般性，本文将未知的 3D 光照环境 $\Psi$ 表示为环境照明 $E$ 和一组点光源 $\mathcal{P} = { \vec{p}_i \mid i \in {1, 2, \dots, K} }$

\[\begin{equation} \Psi=\{E,\mathcal{P}\}, \end{equation}\]

其中 $E$ 是高动态范围图（HDRI）。点光源 $\vec{p}_{i} \in \mathbb{R}^{6}$ 被定义为非负 RGB 强度与不受约束的 3D 位置的 concatenation。

Objective function. 目标是在 PBR 环境中使用 textured mesh $M$ ，通过最优化 3D 光照环境 $Psi$ 尽可能的重建 $D$，训练的目标函数可以定义如下：

\[\begin{equation} e(D,M,\Psi)=\sum_{\forall i\in\mathcal{V}}\sum_{\{r,g,b\}}\left(D_i-\mathrm{pbr}(M,\Psi)_i\right)^2, \end{equation}\]

其中 $\mathrm{pbr}(M, \Psi)$ 表示基于物理的渲染操作，以及 $\mathcal{V}$ 是渲染中的合法像素组，但不包括单目几何估计产生的空洞。

Optimization.

Neural renderer

流程的最后一步是前馈神经渲染器 (NR)，它模拟初始渲染 $\tilde {D}$ 与真实世界外观之间的差距。给定图像 $𝐼$，首先生成场景的光照不变的 3D 表示，然后在 CG 光照下进行渲染。使用漫反射图像 $𝐷$ 作为目标变量，生成与环境中原始光照最接近的 PBR 近似值。$𝐼$ 本身作为真实世界外观的 ground-truth。利用物理建模为 NR 生成光照相关的输入，从而有效地将其与 $𝐼$ 中的现有光照分离。光照变量 $𝐼$ 和 $𝐷$ 仅用作 NR 或 PBR 的目标变量。

Input and losses.

初次渲染 $\tilde {D}$ 能够反映目标光照条件，但缺乏细节。为了能够让网络保持原始场景内容的高保真度，还将 diffuse reflectance $A$ 作为输入。如上一节中提到的，由于不完整的 geometry 会导致在 PBR 结果中丢失部分像素，为此使用了一个 low-level hole 来进行填充，以清除 $\tilde {D}$ 中的一些高频伪影，且将一个非合法像素的二值掩码 $\mathcal{V}^{c}$ 作为输入。最后将 $D, A, \mathcal{V}^{c}$ 在通道维度上进行相加以得到一个 7-通道数的 map 来作为 NR 的输入。

NR 的输入结果 $\hat{I}$ 被定义在线性RGB空间中的真实世界的重光照结果。使用原始图像 $I$ 作为输入，损失函数结合了多尺度梯度损失以及MSE重建损失，整个损失函数定义如下：

\[\begin{equation} \mathcal{L}=MSE(I,\tilde{I})+\sum_\boldsymbol{m}MSE(\nabla I^\boldsymbol{m},\nabla\tilde{I}^\boldsymbol{m}), \end{equation}\]

其中 $\nabla I^\boldsymbol{m}$ 表示输入图像 $I$ 在尺度 $m$ 下的梯度。