Latent Bridge Matching for Fast Image-to-Image Translation
论文链接:LBM: Latent Bridge Matching for Fast Image-to-Image Translation
Architexture
Abstract
现有的扩散模型在img2img任务中需要多步才能达到比较好的效果,虽然已经有蒸馏或者流方法来加速采样过程,但是任然无法实现单步生成。因此,本文基于Latent Space 中的 Bridge Matching,来实现单步img2img
Introduction and Related work
Diffusion Models
- 迭代生成效率低:需要多步去噪(如50步),无法满足实时需求。
- 任务泛化性差:现有加速方法(如蒸馏)主要针对文本到图像任务,难以迁移到其他图像转换任务。
Flow Matching and Bridge Matching:
- 像素空间计算成本高:直接在高分辨率像素空间建模导致计算复杂度高。
- 泛化能力受限:现有方法在低分辨率图像上表现良好,但难以扩展到高分辨率或复杂任务。
创新点与主要贡献创新点:
潜在桥匹配(LBM):将桥匹配框架与潜在空间结合,解决高分辨率图像的计算瓶颈。
条件扩展:引入光照图等条件输入,支持可控图像生成(如阴影位置、光源颜色)。
Method
Bridge Matching
设 $\pi_{0}$ 和 $\pi_{1}$ 是两个概率分布,Bridge Matching的主要思想是,找到一个映射 $f$,使得能够从一个分布 $\pi_{0}$ 从采样得到样本 $x_{0}$ 后,通过映射 $f$ 得到另一个分布 $\pi_{1}$ 中的样本 $x_{1}$ 。因此为了达到这个目的,建立一个随机插值 $x_{t}$,使得在给定 $(x_{0}, x_{1})$ 的情况下, $x_{t}$ 的条件分布 $\pi(x_{t}|x_{0},x_{1})$ 本质上是一个布朗运动(也称为布朗桥),插值公式如下表示:
\[\begin{equation} x_{t} = (1-t)x_{0}+tx_{1}+\sigma\sqrt{t(1-t)}\epsilon \end{equation}\]其中,$\epsilon \sim \mathcal{N}(0,I)$,$\sigma \ge 0$, 且 $t\in[0,1]$。值得注意的是,如果进一步设 $\sigma=0$,就可以得到流匹配公式,其可被视为Bridge Matching的零噪声极限。因此,$x_{t}$ 随时间的演化由以下随机微分方程(SDE)给出:
\[\begin{equation} dx_t = \frac{x_1-x_t}{1-t}d_t+\sigma dB_t, \end{equation}\]其中 $v(x_t,t)=(x_1-x_t) /(1-t)$ 被称为随机微分方程的漂移项。为了从分布 $\pi_{0}$ 中采样得到分布 $\pi_{1}$ 的样本,使用随机微分方程SDE时需要确保 $x_t(\pi_{t})$ 的分布是马尔可夫的,即不依赖于 $x_{1}$ 。在实际操作中,会进行马尔可夫投影,通常包括使用神经网络对随机微分方程的漂移项进行回归,训练目标为最小化如下函数:
\[\begin{equation} \mathbb{E}_{t,x_{0},x_{1}}\left [ ||(x_1-x_t) /(1-t)-v_{\theta}(x_t,t)|| \right ] . \end{equation}\]最后,估计出的漂移函数 $v_{\theta}$ 可以被整合到标准的随机微分方程求解器中,用于求解SDE,从而从分布 $\pi_{0}$ 中抽取的初始样本 $x_{0}$ 出发,生成服从分布 $\pi_{1}$ 的样本 $x_{1}$ 。
Latent Bridge Matching
类似于Stable Diffusion,应用VAE后,可以顺势地将pixel space中的扩散模型拓展到隐空间中,隐空间中的桥匹配模型的训练目标可以表示如下: \(\begin{equation} \mathcal{L}_{\mathrm{LBM}}=\mathbb{E}\left[\left\|(\mathcal{E}(x_1)-\mathcal{E}(x_t))/(1-t)-v_\theta(z_t,t)\right\|^2\right] \end{equation}\)
在推理时,可以使用来自 $\pi_{0}$ 的样本实现从分布 $\pi_{1}$ 中进行采样。具体而言,首先从 $\pi_{0}$ 中抽取一个样本,将其映射到潜在空间,使用标准随机微分方程 (SDE) 求解器,即求解公式 (2) 中的随机微分方程 (SDE),然后使用 VAE 的解码器将潜在空间映射回图像空间。这种方法的优点是通过降低数据的维度来大幅降低计算成本,从而允许训练可扩展到高维数据(例如高分辨率图像)的模型。需要注意的是,计算来自 $\pi_{0}$ 或 $\pi_{1}$ 的任何样本相关的潜在空间可以在训练之前完成。类似于针对扩散模型提出的方法,可以推导出 LBM 的条件设置。在这种情况下,除了 $(x_0,x_1)$ 配对之外,还引入了一个额外的条件变量 $c$,它将进一步指导生成过程。因此, $v_{\theta}$ 是关于 $c$ 进行调节的,因此 $v_{\theta}(z_t,t,c)$ 也取决于条件变量 $c$。
Training detail
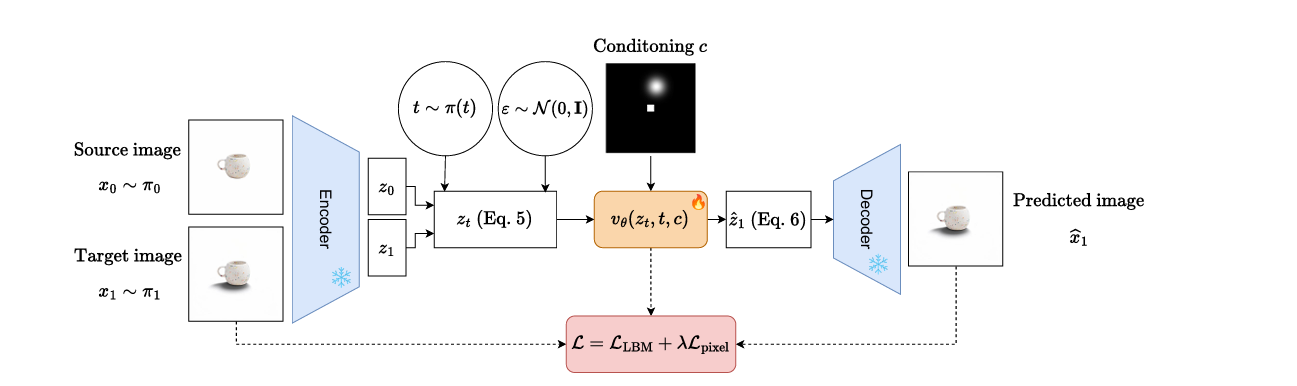
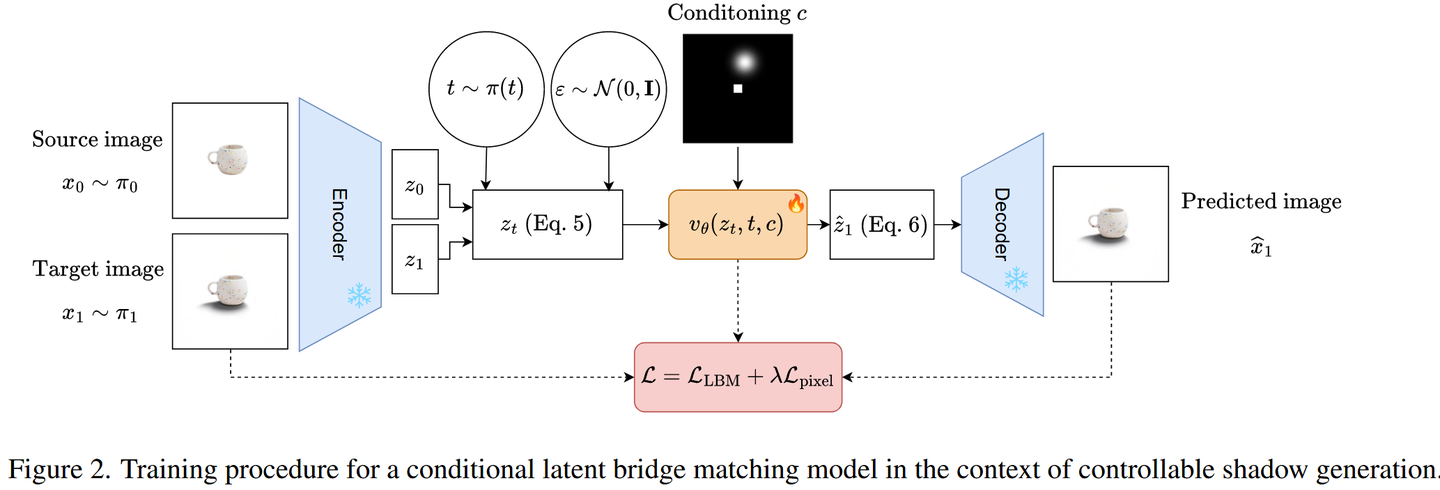
现假设有两个图像分布 $\pi_{0}$ 和 $\pi_{1}$,现想要将样本从 $\pi_{0}$ 转移到 $\pi_{1}$。训练过程如下:首先,抽出一对样本数 $x0,x1) ∼ \pi_{0} \times \pi_{1}$。然后这些样本将被预先训练的 VAE 给出编码到相应的潜变量 $z_{0}$ 和 $z_{1}$。从 $\pi(t)$ 得到时间步长 $t$ ,使用方程(5)得到时间步分布和噪声样本 $z_{t}$。然后将此样本,即将 $z_{t}$ 传递给降噪器 $v_{\theta}(z_{t},t)$,该降噪器会根据时间步 $t$ 进行额外调节并预测 drift 。值得注意的是,可以很容易地根据预测的 drift 得到相应预测潜在变量 $z_{1}$: \(\begin{equation} \hat{z_{1}} = (1-t)\cdots v_{\theta}(z_{t},t) + z_{t}. \end{equation}\) 在训练期间,作者还引入了一个像素损失像素。损失包括解码估计的目标潜在 $x_{1}= \mathcal{D}(z_{1})$,其中 $\mathcal{D}$ 是 VAE 的解码器,并将其与实际 目标图像 $x_{1}$。损失函数有多种选择,例如 L1、L2 或 LPIPS 。作者发现 LPIPS 在实践中效果很好,可以加速域转移。为了随图像大小缩放,作者制定了随机裁剪策略,并且仅在图像大小大于特定阈值时计算patch上的损失。这限制了模型的内存占用,因此它不会成为训练效率的负担。最终目标可以总结如下: \(\begin{equation} \mathcal{L}=\mathcal{L}_{\mathrm{LBM}}(\mathcal{E}(x_{0}),\mathcal{E}(x_{1}))+\lambda\cdot\mathcal{L}_{\mathrm{pixel}}(\widehat{x}_{1},x_{1}). \end{equation}\) 作者在图 2 中提供了条件设置中建议的方法。为了便于说明,作者选择了可控阴影生成的上下文,其中生成进一步受到指示光源位置的光照贴图 $c$ 的限制源。在此设置中,$\pi_{0}$ 对应于与无阴影图像关联的潜在分布,而 $\pi_{1}$ 是与有阴影的图像关联的潜在分布。在训练过程中,可以通过沿通道维度连接潜在变量 $z_{t}$ 来将条件变量 $c$ 注入降噪器 $v_{\theta}$。
下面是代码实现部分,整个用于训练的模型由一个类 LBModel实现,而训练的逻辑主要在其前向函数 forward中实现:
首先是采样时间步以及其变量 $\sigma$:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
## 采样时间步
timestep = self._timestep_sampling(n_samples=z.shape[0], device=z.device)
sigmas = None
## _timestep_sampling函数实际上就是返回一个时间步timestep:
## training_noise_scheduler 默认使用流匹配欧拉调度器:FlowMatchEulerDiscreteScheduler
def _timestep_sampling(self, n_samples=1, device="cpu"):
if self.timestep_sampling == "uniform":
idx = torch.randint(
0,
self.training_noise_scheduler.config.num_train_timesteps,
(n_samples,),
device="cpu",
)
return self.training_noise_scheduler.timesteps[idx].to(device=device)
elif self.timestep_sampling == "log_normal":
u = torch.normal(
mean=self.logit_mean,
std=self.logit_std,
size=(n_samples,),
device="cpu",
)
u = torch.nn.functional.sigmoid(u)
indices = (
u * self.training_noise_scheduler.config.num_train_timesteps
).long()
return self.training_noise_scheduler.timesteps[indices].to(device=device)
elif self.timestep_sampling == "custom_timesteps":
idx = np.random.choice(len(self.selected_timesteps), n_samples, p=self.prob)
return torch.tensor(
self.selected_timesteps, device=device, dtype=torch.long
)[idx]
随后是创建方程 $x_{t} = (1-t)x_{0}+tx_{1}+\sigma\sqrt{t(1-t)}\epsilon$:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# Get inputs/latents
## z: target_key, while z_source:source_key
if self.vae is not None:
vae_inputs = batch[self.target_key]
z = self.vae.encode(vae_inputs)
downsampling_factor = self.vae.downsampling_factor
else:
z = batch[self.target_key]
if self.vae is not None:
z_source = self.vae.encode(source_image)
else:
z_source = source_image
## _get_sigmas函数实际是返回一个和latent维度相同的sigma
def _get_sigmas(
self, scheduler, timesteps, n_dim=4, dtype=torch.float32, device="cpu"
):
sigmas = scheduler.sigmas.to(device=device, dtype=dtype)
schedule_timesteps = scheduler.timesteps.to(device)
timesteps = timesteps.to(device)
step_indices = [(schedule_timesteps == t).nonzero().item() for t in timesteps] ## 从schedule_timesteps中获取与timesteps有相等的值的索引列表
sigma = sigmas[step_indices].flatten() ## 展平
while len(sigma.shape) < n_dim:
sigma = sigma.unsqueeze(-1)
return sigma
# Create interpolant
sigmas = self._get_sigmas(
self.training_noise_scheduler, timestep, n_dim=4, device=z.device
)
##
noisy_sample = (sigmas * z_source + (1.0 - sigmas) * z + self.bridge_noise_sigma * (sigmas * (1.0 - sigmas)) ** 0.5 * torch.randn_like(z))
for i, t in enumerate(timestep):
if t.item() == self.training_noise_scheduler.timesteps[0]:
noisy_sample[i] = z_source[i]
最后是预测噪声和预测样本,以及损失函数:
1
2
3
4
5
6
7
8
9
10
11
# 使用去噪器预测噪声
prediction = self.denoiser(
sample=noisy_sample,
timestep=timestep,
conditioning=conditioning,
*args,
**kwargs,
)
target = z_source - z ## z_1 - z_t
denoised_sample = noisy_sample - prediction * sigmas
Dataset
重光照与阴影生成:
- 合成数据主导:使用Blender渲染3D模型,结合随机HDR光照图生成配对数据。
- 真实数据增强:通过图像分割提取前景,结合IC-Light模型生成重光照效果。
这项任务颇具挑战性,因为大多数情况下并不存在这样的图像对,即前景完全相同但背景不同(因此光照条件也不同)的图像。由于无法获得此类数据,因此依赖于以下数据创建策略。
首先收集了一组公开可用且可免费使用的图像,这些图像都具有显著的前景,并使用Birefnet为每幅图像计算前景mask,从而得到一组图像 $\mathcal{X}$。然后,给定一对图像 $x_1,x_2 \in \mathcal{X}$,利用 $x_1$(对应为 $x_2$)的前景和 IC-Light 模型,根据 $x_2$(分别为 $x_1$)的背景,生成重新光照的前景 $x_{1}^{fg}$(对应为 $x_{2}^{fg}$)。最后,将 $x_{1}^{fg}$ 和 $x_{2}^{fg}$ 粘贴回原始图像 $x_{1}$ 和 $x_{2}$ 上以生成源图像 $y_1$ 和 $y_2$,同时将 $x_1$ 和 $x_2$ 作为目标图像。
此外,还依赖于使用渲染引擎 Blender 创建的合成数据。合成数据集创建过程始于整合各种 3D 物体和人体模型以及 HDR 图像。然后,这些元素将用于渲染高质量的图像。对于物体,从 BlenderKit 平台收集了大量高质量的 3D 模型,该平台拥有专业制作的素材资源,并提供免费使用许可。对于人体,使用 Blender 插件,通过随机定制面部特征、体形、姿势、发型和服饰选项来生成独特的 3D 人体模型。在数据集创建过程的每次迭代中,首先随机选择一个 3D 模型。然后,随机选择 HDR 图像来照亮前景物体。渲染场景,并保存图像和相关的前景蒙版,得到 $x_1$。使用另一个 HDR 贴图执行相同操作,但使用相同的 3D 物体,得到 $x_2$。最后,可以将 $x_1$ 的前景粘贴到 $x_2$ 上,反之亦然,从而创建源图像 $y_2$ 和 $y_1$,并再次使用 $x_1$ 和 $x_2$ 作为目标图像。数据集中的示例渲染如图 4 所示。
物体移除:
- 真实数据:RORD数据集(带掩码的物体-背景配对图像)。
- 合成数据:Blender生成3D模型,随机掩码并渲染。
- In-the-wild数据:随机掩码自然图像,部分掩码区域无物体(强制模型学习背景修复)。
省流版: